WSL2でJModelicaのDockerを動かす
はじめに
JModelicaのDockerイメージを使ってBuildingsライブラリを使う際のメモ。JModelicaは開発は終了しているものの、Modelonが公開はしているのでJModelicaを使う際に必ずしもこのDockerイメージを使う必要はない。
Buildingsライブラリ自体はOpenModelicaのnightlyビルド版を使えばだいぶ使えるようになっている。しかし、SOEPでFMIを使う場合はDymolaかJModelicaかOPTIMICAを使う必要があるようなので、現在この中で唯一無償で使えるJModelicaの需要はまだある。なお、SOEP用にOPTIMICAを無償で使えるように頑張っているらしいので、いずれはOPTIMICAを使うことになるかもしれない。
Windows用のDockerとしてDocker Desktop for Windowsがあり個人使用の範囲ではライセンスも問題ないのだが、今回使用するDockerの起動用スクリプトがシェルスクリプトなので、wsl2から実行することにする。
環境構築
WSL2のインストールはここを見ればできると思うけれど、基本的に管理者権限のPowerShellで以下を実行するだけである。もしかすると、古い環境だともう少し手間をかける必要があるかもしれない。
wsl --install
DockerのWSL2へのインストールはここに書いている通りにやる。先ほどインストールしたUbuntuを開いて以下を実行する。
sudo apt-get update sudo apt-get install \ ca-certificates \ curl \ gnupg \ lsb-release curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo gpg --dearmor -o /usr/share/keyrings/docker-archive-keyring.gpg echo \ "deb [arch=$(dpkg --print-architecture) signed-by=/usr/share/keyrings/docker-archive-keyring.gpg] https://download.docker.com/linux/ubuntu \ $(lsb_release -cs) stable" | sudo tee /etc/apt/sources.list.d/docker.list > /dev/null sudo apt-get update sudo apt-get install docker-ce docker-ce-cli containerd.io
これでDockerがインストールできた。ただし、そのまま公式の説明通りにHello Worldをやると失敗すると思う。Docker Daemonの起動と停止を行う必要がある。
sudo service docker start sudo docker run hello-world sudo service docker stop
JModelicaのDockerを動かす
ここからUbuntuでJModelicaのイメージを動かすには公式の説明に従えばよい。このリポジトリに加え、Buildingsライブラリもダウンロードする必要がある。
cd ~ mkdir modelica cd modelica git clone https://github.com/lbl-srg/docker-ubuntu-jmodelica.git wget https://github.com/lbl-srg/modelica-buildings/releases/download/v8.1.0/Buildings-v8.1.0.zip unzip Buildings-v8.1.0.zip mv './Buildings 8.1.0' ./docker-ubuntu-jmodelica/Buildings
本来はBuildingsはライブラリ用のフォルダに移動すべきな気がするが、ライブラリ内のチュートリアルを実行する都合上このような場所にしている。自分のモデルを作って実行するなら切り分けるとよいと思う。その際はexport MODELICAPATH="~/modelica/lib/Buildings"といった記述を~/.bashrcファイルに書いておくと良い。
計算を実行用のシェルスクリプトjm_ipython.shはMODELICAPATHやPYTHONPATHをDockerの環境に渡す処理をしているだけらしい(PYTHONPATHは何に使ってるのだろう)。以下のようにして計算を実行する。
cd ./docker-ubuntu-jmodelica sudo service docker start sudo ./jm_ipython.sh jmodelica.py Buildings.Utilities.Psychrometrics.Examples.DewPointTemperature sudo service docker stop
計算結果はBuildings_Utilities_Psychrometrics_Examples_DewPointTemperature_result.matである。OpenModelicaやJModelicaやBuildings.pyなどの好きな環境で閲覧するとよい。wsl上のファイルは\\wsl$\Ubuntu\home\username\modelica\docker-ubuntu-jmodelicaみたいなパスでWindowsのエクスプローラーからも確認でき、ドラッグ&ドロップでWindows側に持ってくることもできる。パスのusernameはwslでの自分の名前で、Ubuntuのところにバージョン名がはいってたりするかもしれない。
ちなみに今計算したファイルは絶対湿度を変化させたときの露点温度を計算するものであった。以下が入力条件をOpenModelicaで開いて確認したもの。
 以下が露点温度。絶対温度なので273.15を引いてやると摂氏温度になる。
以下が露点温度。絶対温度なので273.15を引いてやると摂氏温度になる。

また、ログファイルとしてBuildings_Utilities_Psychrometrics_Examples_DewPointTemperature_log.txtの他にBuildings_Utilities_Psychrometrics_Examples_DewPointTemperature_html_diagnosticsフォルダにいろいろhtmlが出力されている。デバッグする際にはいろいろ役に立つと思う。デバッグの際にはsudo ./jm_ipython.sh -i jmodelica.py Buildings.Utilities.Psychrometrics.Examples.DewPointTemperatureとiオプションをつけるとインタラクティブモードになってjmodelica.pyを実行した後の状態でipythonを起動したままになる。これで値を確認するなどができ、exit()で終了する。
ソルバーの設定はjmodelica.pyの中で行っている。ncpが500だったりするので必要に応じて値を編集する必要があると思う。普段VSCodeを使っているならcode jmodelica.pyとすればWindowsのVSCodeでWSL上のファイルを簡単に編集できる。オプションの設定についてはJModelicaのマニュアルを見る必要があるので結局JModelicaをダウンロードしたほうが良いかもしれない。一応JModelicaの中のFMI実行部分にあたるPyFMIのHPのドキュメントを見ることもできる。スクリプト上のmodがpyfmi.fmi.FMUModelME2クラス、optsがpyfmi.fmi_algorithm_drivers.AssimuloFMIAlgOptionsクラスのインスタンスである。おそらく多くのケースではncp以外にres = mod.simulate(options=opts, start_time=0, final_time=604800)とするなど計算時間関係を指定するぐらいで、他のソルバーのパラメータなどは基本的にいじらなくてもよい気はする。
引数のモデル名は以下のようにファイル名で与えてもよいようになっている。
if len(sys.argv) > 1:
# If the argument is a file, then parse it to a model name
if os.path.isfile(sys.argv[1]):
model = sys.argv[1].replace(os.path.sep, '.')[:-3]
else:
model=sys.argv[1]
Buildings/Utilities/Psychrometrics/Examples/DewPointTemperature.moがBuildings.Utilities.Psychrometrics.Examples.DewPointTemperatureになるようになっている。そのため、カレントディレクトリ直下からのパスじゃないとうまく動かないと思われる。
おわりに
WSL2でJModelicaのDockerを使った計算方法を確認した。今後SOEPの計算について調べていきたい。
BuildingsPyを使う
概要
今回はJupyter上でJModelicaを動かしながらBuildingsPyを使ってみる。JModelicaはバージョン2.14でOSSでの開発は終了したが、まだOpenModelicaでは動かない時も多いので今後もしばらく使うことになる。バージョン2.14のリリースノートに次はpython3系にすると書いてたけれどpython2系のままになってしまったのが残念。
BuildingsPyは以下の事ができる。今回は上の3つを使ってみる。
- FMUの変数間の依存関係の集計。
- matファイルの読み込み。Dymolaでなくても一応読めている。
- matファイルのデータから箱ひげ図のプロット。matplotlibのboxplotの設定をしている。
- Dymolaでの計算の実行。他の環境は対応していない。
- 開発用のリファクタリングやリグレッションテスト、moファイルのhtmlのチェックなど。
実行環境
- Windows10 Pro 64bit
- JModelica 2.14 →Modelica標準ライブラリ(MSL) 3.2.2
- Buildings 6.0.0
準備
ファイルやフォルダの位置は参考位置なので個人の好きなところでもよいと思われるが、名前にスペースを入れるのは避けた方が無難。
JModelicaの用意
JModelicaをJupyter上で実行できる環境を用意する。finbackさんがJupyterでのJModelica実行について書いてくださっているので、実行環境の準備はこれを見れば問題ない。また、UedaさんがJupyterでのOpenModelicaの実行も書いてくださっているのでOpenModelica派の人はこちらもよいと思う。
BuildingsPyのインストール
JModelicaをJupyterで立ち上げて以下を入力して実行。
!pip install buildingspy
pandasなども入れてなければ入れる。
Buildingsライブラリの用意
まずBuildingsライブラリをダウンロードして解凍し、%USERPROFILE%\JModelica\libにおく。%USERPROFILE%は'C:\Users\ユーザー名'の事である。 フォルダ名のスペースが気になるので、フォルダ名からバージョン番号を抜いておく。
ライブラリのパスの設定として、JModelicaのJupyterの起動用のbatファイルの
"%PYTHONHOME%\python.exe" -m jupyter notebook %*
の前に以下の一行を加えて保存する。
set MODELICAPATH=C:\JModelica.org-2.14\install\ThirdParty\MSL;%USERPROFILE%\JModelica\lib
計算ファイル
計算ファイルはBuildingsライブラリのサンプルファイルをそのまま使う。%USERPROFILE%\JModelica\lib\Buildings\Examples\Tutorial\SpaceCooling\System3.moを作業フォルダにコピーしてくる。このままだと動かないので適当なテキストエディタなどでファイルを開いて113行と120行のBoundaryConditionsの前にBuildings.をつける。さらに後から気象データを入れ替えたいときにデフォルトの記述のままだとどうもうまくできなかったので116行を以下のように直接ファイル名を指定するように書き換えて保存。
filNam="C:/Users/Simulation/JModelica/lib/Buildings/Resources/weatherdata/USA_IL_Chicago-OHare.Intl.AP.725300_TMY3.mos",
気象データ
気象データとしてepwファイルをダウンロードし、%USERPROFILE%\Documents\JModelica\work\lib\Buildings\Resources\weatherdataにおく。
以下のようにしてepwファイルをmosファイルに変換する。Javaのパス廻りはすでにJavaが入っていて設定できている人には不要かもしれない。
cd %USERPROFILE%\JModelica\lib\Buildings\Resources\weatherdata set PATH=%PATH%;C:\JModelica.org-2.14\Java\jdk-11.0.2\bin set JAVA_HOME=C:\JModelica.org-2.14\Java\jdk-11.0.2 java -jar ../bin/ConvertWeatherData.jar JPN_Nagoya.476350_IWEC.epw
JPN_Nagoya.476350_IWEC.mosファイルができる。
計算の内容
以下の2つのファイルが用意できているはず。
%USERPROFILE%\JModelica\lib\Buildings\Resources\weatherdata\JPN_Nagoya.476350_IWEC.mos
%USERPROFILE%\JModelica\work\buildingspy\System3.mo
System3.moの内容は以下の通り。
- 単室の室温の計算。
- 壁や天井など外皮は定常計算モデルとし、1枚にまとめている。
- 日射や長波放射は無視。
- 室内の空気に一定発熱を与えている。
- 熱回収した外気を冷水コイルで冷却してオンオフ制御で空調。
実行時には以下の2点をデフォルトから変更する。
- 読み取る外気の気象データを名古屋のものに変更。
- 計算は30日分を1分刻みで計算するよう変更。
Jupyter notebookの内容は以下の通り。変数の数が多くて読みづらくなってしまった。
- 計算の実行
- 通常通りグラフの描画
- Buildingspyの操作の確認
- matファイルのデータをcsvで出力
Buildingspyの操作について
せっかく計算時間を長くしてみたのだけれど、箱ひげ図のプロットがどうも上手くいかなかった。普通に読み込んだmatファイルのデータをmatplotlibでグラフを書けばよいのだと思う。一応以下の事は出来た。痒い所をちょっぴり補助してくれるといった印象。
- fmuファイルの変数間の依存関係の一覧化(使いどころがまだ良く分からない)
- matファイルの変数名を正規表現で検索して表示
- matファイルのデータの時間積分(合計)、時間平均、最大、最小の表示
- 時間間隔を変更してmatファイルのデータを抽出or線形補間
- matファイルのデータをcsvで出力
まとめ
BuildingsPyは正規表現での変数名の検索とmatファイルのデータを任意の時間で取り出せるのが使いやすくて便利だと感じた。matファイルはJModelicaのPlot-GUIやOpenModelicaで結果の確認をしても良いのだけれど、今回のやり方だとpythonでそのまま加工できスクリプトの流用も簡単で良いと感じた。DyMatというライブラリもありそれはfinbackさんの記事で使い方を紹介してくれているのでそちらを使っても良いとは思う。
Jupyterでの実行が気に入ったので少しずついろいろ動かしていきたい。
The Modelica Buildings library 6.0.0リリースノート
概要
2019年7月15日にLBNLからThe Modelica Buildings library 6.0.0がリリースされました。ライブラリのテスト環境はDymola 2019FD01、Dymola 2020、JModelica (revision 12903)です。これまで通りOpenModelicaはテストの対象外です。
個々の要素の詳細な確認は置いておいて、取り急ぎ翻訳して概要だけ把握をします。
リリースノートの原文はこちら
主な変更
- 在室者の行動モデルのパッケージの追加
- 地中熱利用のボアホールのパッケージの追加
- 日射遮蔽や屋外照明の制御用のブロックのパッケージの追加
- 時系列プロットと散布図を生成し、htmlファイルへ書き出すブロックのパッケージの追加
- 単位変換用のブロックのパッケージの追加
- Buildings.Controls.OBC.CDLに数種類の新しいコントロールブロックの追加
在室者の行動モデルはIEA EBC Annex 66のものも取り入れられているようです。IEA EBC Annex 66のテーマはDefinition and Simulation of Occupant Behavior in Buildingsで建物内の人間の行動モデルの定義を行っています。日本のContributorsとしては大阪大学の山口容平准教授が名を連ねており日本人の特性も少しは考慮されているかもしれません。(そういうものがあるのかどうかも知りませんが。。。)
変更の一覧
紛らわしいですが、単にissueを参照というのはこちらのリポジトリのことで、IBPSAのissueを参照というのはこちらのリポジトリのことです。
パッケージの追加
| 名称 | 説明 |
|---|---|
| Buildings.Controls.OBC.OutdoorLights | 屋外照明のコントローラー |
| Buildings.Controls.OBC.Shade | 日射遮蔽のコントローラー |
| Buildings.Controls.OBC.UnitConversions | 単位変換用のブロックのパッケージ。Modelicaと異なる単位系のBASのデータを読み書きする際に使用する事を意図している。 |
| Buildings.Fluid.Geothermal | 地中熱熱交換器のモデルのパッケージ。このパッケージには、垂直ボアホールを備えたボアフィールドと、U字管熱交換器を備えた単一の垂直ボアホールのモデルがある。ボアフィールドモデルでは、任意の幾何学的構成、および1つまたは2つのU字管熱交換器を持つことができる。 |
| Buildings.Occupants | 在室者の行動のモデルと関数のパッケージ。住居やオフィスビルの冷暖房システム、窓、ブラインド、照明と在室者との相互作用や在室状況を計算する。 |
| Buildings.Utilities.Cryptographics | SHA1暗号化文字列を計算する関数のパッケージ。 |
| Buildings.Utilities.IO.Files | files.CSVファイル、JSONファイル、またはコンビタイムテーブルファイルを書き込むためのブロックのパッケージ。 |
| Buildings.Utilities.Plotters | 時系列プロットと散布図を生成し、これらのプロットを1つまたは複数のhtmlファイルに書き込むブロックのパッケージ。プロットは入力信号および時間遅延に基づいて無効にすることができ、例えば、HVACシステムが少なくとも30分間動作している間にのみデータをプロットすることができる。 |
既存ライブラリへのコンポーネントの追加
Buildings.Controls.OBC.CDL.
| 名称 | 説明 |
|---|---|
| Continuous.MultiOr | ブール入力ベクトルのいずれかの要素がtrueの場合に限り、trueを出力するブロック。 |
| Continuous.MatrixMin | 行方向または列方向の最小値のベクトルを出力するブロック。 |
| Continuous.MatrixMax | 行方向または列方向の最大値のベクトルを出力するブロック。 |
| Continuous.MatrixGain | ゲイン行列と入力信号ベクトルの積を出力するブロック。 |
| Discrete.MovingMean | サンプリングされた入力信号の離散移動平均を出力するブロック。 |
| Integers.Change | Integer入力がその値を変更したかどうか、そして増加または減少したかどうかを出力するブロック。 |
| Logical.IntegerSwitch | ブール入力信号に基づいて2つの整数入力信号のうちの1つを出力するブロック。 |
| Routing.RealExtractor | 整数値入力に依存する信号ベクトルからスカラー信号を抽出するブロック。 |
| Utilities.SunRiseSet | 毎日の日の出と日の入り時刻を出力するブロック。 |
Buildings.Fluid.
| 名称 | 説明 |
|---|---|
| HeatExchangers | 設計条件と現在の質量流量に基づいてプレート式熱交換器の効率を計算するBuildings.Fluid.HeatExchangers.PlateHeatExchangerEffectivenessNTUを追加。 |
Buildings.Utilities.
| 名称 | 説明 |
|---|---|
| Math | ベッセル関数、指数積分、階乗、下降階乗、二項関数の追加。 |
| Psychrometrics.Functions.X_pTphi | 与えられた圧力、温度および相対湿度に対する湿気の質量分率を計算する関数の追加。 |
後方互換性を維持した既存コンポーネントの改善
Buildings.BoundaryConditions.
| 名称 | 説明 |
|---|---|
| WeatherData.ReaderTMY3 | 1年未満で新年にまたがる気象データ、および1年以上にわたる気象データに対応するように実装を更新。IBPSAのissue#842を参照。 |
Buildings.Controls.OBC.CDL.
| 名称 | 説明 |
|---|---|
| Logical.Timer | 入力がtrueの場合に累積時間を出力するように実装を更新。issue#1212を参照。 |
| Logical.TrueDelay | 初期のtrueの入力をオプションで遅らせるパラメータdelayOnInitを追加。issue#1346を参照。 |
Buildings.Controls.OBC.ASHRAE.G36_PR1.
| 名称 | 説明 |
|---|---|
| AHUs.SingleZone.VAV.SetPoints.OutsideAirFlow | 在室センサーがない場合に在室者数を入力として設定しなくても済むように、在室用の入力コネクターを条件によって取り外しするよう変更。issue#1270を参照。 |
Buildings.Fluid.
| 名称 | 説明 |
|---|---|
| Interfaces.ConservationEquation MixingVolumes.MixingVolume MixingVolumes.MixingVolumeMoistAir |
ボリュームがコンパイル時に修正されないようにモデルを変更。issue#1411を参照。 |
Buildings.Media.
| 名称 | 説明 |
|---|---|
| Air Water Antifreeze.PropyleneGlycolWater Specialized.Air.PerfectGas |
温度または質量分率が許容範囲外の場合のエラーメッセージを修正。IBPSAのissue#1045を参照。 |
Buildings.Utilities.IO.Python27.
| 名称 | 説明 |
|---|---|
| Functions.exchange | PYTHONPATH環境変数の設定をリファクタリング。issue#1421を参照。 |
後方互換性を伴わない既存コンポーネントの改善
Buildings.Airflow.Multizone.
| 名称 | 説明 |
|---|---|
| DoorDiscretizedOperable | パラメータCDを削除。Dymolaの場合は、変換スクリプトによってこの変更を行う。IBPSAのissue#971を参照。 |
| EffectiveAirLeakageArea | パラメータA、CD、およびlWetを削除。Dymolaの場合は、変換スクリプトによってこの変更を行う。IBPSAのissue#932を参照。 |
| MediumColumnDynamic | パラメータm_flow_nominalを削除。Dymolaの場合は、変換スクリプトによってこの変更を行う。IBPSAのissue#970を参照。 |
| Orifice | パラメータlWetを削除。Dymolaの場合、変換スクリプトによってこの変更を行う。IBPSAのissue#932を参照。 |
| MediumColumnDynamic MediumColumn EffectiveAirLeakageArea Orifice |
これらのモデルでは意味がないので、allowFlowReversalパラメータを削除。Dymolaの場合は、変換スクリプトによってこの変更を行う。IBPSAのissue#877を参照。 |
Buildings.BoundaryConditions.
| 名称 | 説明 |
|---|---|
| WeatherData.BaseClasses.ConvertTime | 複数年にわたる気象データに必要な新しいパラメータを追加。このモデルは、すべての必要な変更を実装する気象データファイルリーダーの一部であるため、ユーザーがこの変更の影響を受けることはほとんどない。IBPSAのissue#842を参照。 |
Buildings.Controls.OBC.ASHRAE.
| 名称 | 説明 |
|---|---|
| G36_PR1.AHUs.SingleZone G36_PR1.AHUs.MultiZone |
パッケージの名前をG36_PR1.AHUs.SingleZone.VAVおよびG36_PR1.AHUs.MultiZone.VAVに変更し、一貫性を保つためにさまざまな信号とパラメータの名前を変更。Dymolaの場合は、変換スクリプトによってこの変更を行う。 |
Buildings.Controls.OBC.CDL.
| 名称 | 説明 |
|---|---|
| RealExtractSignal | ExtractSignalからブロック名を変更。Dymolaの場合は、変換スクリプトによってこの変更を行う。 |
| Continuous.MultiMax | 出力変数名をyMaxからyに変更。Dymolaの場合は、変換スクリプトによってこの変更を行う。issue#1252を参照。 |
| Continuous.MultiMin | 出力変数名をyMinからyに変更。Dymolaの場合は、変換スクリプトによってこの変更を行う。issue#1252を参照。 |
Buildings.Fluid.
| 名称 | 説明 |
|---|---|
| HeatExchangers.DryEffectivenessNTU | 対流熱伝達係数が空気用であるため、名称をHeatExchangers.DryCoilEffectivenessNTUに変更。Dymolaの場合は、変換スクリプトによってこの変更を行う。使用されていない変数Zを削除。 |
| HeatExchangers.PlateHeatExchangerEffectivenessNTU | 使用されていない変数Zを削除。 |
| HeatExchangers.Ground.Boreholes.BaseClasses.factorial | この関数は新しいGeothermalパッケージで使用されるため、名称をBuildings.Utilities.Math.Functions.factorialに変更。Dymolaの場合は、変換スクリプトによってこの変更を行う。 |
| HeatExchangers.Ground.Boreholes | 新しくGeothermalパッケージを導入するため、パッケージの名前をBuildings.Fluid.Geothermal.Boreholesに変更。Dymolaの場合は、変換スクリプトによってこの変更を行う。 |
| HeatExchangers.RadiantSlabs.BaseClasses.MassFlowRateMultiplier | モデルは新しくGeothermalパッケージで使用されるため、Buildings.Fluid.BaseClasses.MassFlowRateMultiplierに変更。Dymolaの場合は、変換スクリプトによってこの変更を行う。 |
| Sources.FixedBoundary | このモデルは現在廃止されており、将来のリリースで削除される予定。名称をBuildings.Obsolete.Fluid.Sources.FixedBoundaryに変更。代わりにBuildings.Fluid.Sources.Boundary_pTの使用を推奨。Dymolaの場合は、変換スクリプトによってこの変更を行う。 |
Buildings.Media.
| 名称 | 説明 |
|---|---|
| Refrigerants.R410A | 使用されていなかったため、関数pressureSatLiq_Tを削除。IBPSAのissue#995を参照。 |
Buildings.Utilities.Reports.
| 名称 | 説明 |
|---|---|
| Printer printRealArray |
PrinterをBuildings.Utilities.IO.Files.Printerに移動し、printRealArrayをBuildings.Utilities.IO.Files.BaseClasses.printRealArray.Forに移動。Dymolaの場合は、変換スクリプトによってこの変更を行う。この変更は新しく導入されたパッケージBuildings.Utilities.IO.Filesによるもの。 |
致命的な不具合の修正(間違った計算結果を導いていたものなど)
Buildings.Controls.OBC.CDL.
| 名称 | 説明 |
|---|---|
| Logical.Latch | 初期段階で誤った結果を引き起こす実装を修正。issue#1402を参照。 |
| Logical.Toggle | 初期段階で誤った結果を引き起こす実装を修正。issue#1402を参照。 |
Buildings.Fluid.Geothermal.
| 名称 | 説明 |
|---|---|
| Borefields.Data.Soil.SandStone | 間違った熱特性を修正。IBPSAのissue#1062を参照。 |
Buildings.Fluid.HeatExchangers.
| 名称 | 説明 |
|---|---|
| Heater_T SensibleCooler_T |
初期条件の伝達が出来ていなかった部分を修正。IBPSAのissue#1016を参照。 |
Buildings.ThermalZones.Detailed.
| 名称 | 説明 |
|---|---|
| MixedAir | 家具を考慮に入れるなど、室内空気の熱容量を増加させる、パラメータmSenFacを継承するように変更。issue#1405を参照。 |
Buildings.ThermalZones.ReducedOrder.
| 名称 | 説明 |
|---|---|
| RC.ThreeElements RC.FourElements |
屋根のRC要素roofRCを反転してport_bが外側になるように変更。屋根と床の抵抗RRemとRは、ドキュメント内で切替。IBPSAのissue#997を参照。 |
些末な不具合の修正(ドキュメントや単位の記載の誤りなど)
Buildings.Controls.OBC.ASHRAE.
| 名称 | 説明 |
|---|---|
| G36_PR1.Generic.SetPoints.OperationMode | パラメータのドキュメントの誤った時間を修正。issue#1409を参照。 |
おわりに
気になるような大きな変更はなさそうです。MixingVolumeでコンパイル時に修正されていたというのは、FMUにしたときに変数であるはずのボリュームの値が変更できなくなることがあり、そうならないように手を加えたようです。履歴をみてもどの部分によりその問題が直ったのかあまりよく分からなかったのですが。。。
今回のアップデートと同時にLBNLが開発しているBuildingsPyの方もバージョン2.0.0へとメジャーアップデートしたようです。こちらはModelica廻りのPythonパッケージで、リリースノートはこちらにあります。
リリースノートに記載はないものの熱交換器のモデルが無事修正されたのでBuildings.Examples.Tutorial.SpaceCoolingがOpenModelicaで実行できるようになったかなと思ったのですが、別のエラーが出ました。OpenModelicaで動かせるに越したことはないと思うので、リポジトリの最新の状態を引っ張ってきて定期的にテストするスクリプトでチェックしながら、対応作業をしていかないとだめですね。
第一回電脳建築最適化世界選手権に参加しませんか

このコンテストの関係者ではないが宣伝してみる。
電脳建築最適化世界選手権(WCCBO:World Championship in Cybanetic Building Optimization)という空気調和衛生工学会主催のコンテストがある。サイトをみるだけでは内容が分かりにくいが一応フライヤーに概要が書いてはある。
参加が決まっている人はマニュアルを読み込めば問題ないので、面白そうなら参加したいという人に向けて全体像を軽く把握できるようにしたいと思う。なお、解釈が間違っている可能性はあるし、今後内容が変更されたりするかもしれない。
概要
このコンテストは誤解を恐れずにざっくり言うと室や熱源の「設定温度の年間のスケジュール」を最適化するコンテストである。
電脳建築最適化というタイトルだが平面プランや構造などの最適化は全く関係がない。「空調制御を最適化して(省エネ性×快適性)の値の大きさを競う」というコンテストである。温度が変われば快適性や機器効率が変わるので上手にバランスを取る必要がある。実物件では条件が揃えられないため、エミュレータを使用して人間の位置や室内環境や熱源システムを模擬することで参加者全員同一条件としている。エミュレータでのバーチャルな世界を想定してるためか「電脳」とついている。デジタルツインのようなものに応用したいのかもしれない。
内容としてはエミュレータ上で設定温度などの年間のスケジュールを決めた「空調制御についての設定ファイル」を提出して「省エネ性×快適性」によるスコアを競うものになる。さらに任意参加ではあるが、リアルタイム(時間はエミュレータ上で圧縮されている)に設定温度を送信して空調制御を行う部門も存在し、自由度が飛躍的に高まることになる。
エミュレータは配布されるので自分で好きなだけ試すことができ、エミュレータ内の時間の進行速度はある程度(1~960倍)調整できる。ただし、管理者権限が必要なので会社で参加したいが権限が貰えない様な場合が仮にあるならば面倒かもしれない。これはBACnet(建築設備の自動制御で使うプロトコル)通信を行うためなのだが、BACnetについての事前知識は全く必要ない。また、任意参加の部門では運営のサーバーにVPN接続を行う必要がある。エミュレータはWindowsの実行ファイルだが、C#のソースコードも配布される。MacやLinuxで自力でビルドするのが現実的かについては現在不明である。
スケジュール
(~4/12金)参加申し込み
参加申し込みが必要で4/12までに申し込む必要がある。参加費なし賞金なし、誰でも匿名でも参加可能でチームでも個人でもよい。資料が郵送されるようなので代表者の住所は必要。
参加申し込み後に資料が送付されるように書いてあるが、すでに公式サイトに資料がアップロードされている。ただし、開始するまでに内容が更新されるかもしれない。
(6/7火)説明会、オフライン部門開始
空衛学会の会議室で説明会のようなものがあるが、参加は任意。遠隔地用に動画の配信があるかもしれない。この日にとりあえず一度提出をして翌日には順位が公開される。
(6/7金~7/7日)オフライン部門
エミュレータ上で年間の空調制御を決めて作成した「空調制御についての設定ファイル」を提出し、主催のサーバー上で計算した結果を競う。6/7に一度提出すればその後何もしなくても問題はない。サーバーでの計算は1日かかるが、期間内であれば何度でも再提出してスコアを更新できる。
(7/8月~8/7水)オンライン部門、任意参加
この期間は運営サーバーでエミュレータの速度を12倍にして1ヶ月で1年間を模擬している。参加者はリアルタイムに状況を把握しながらVPN接続で制御の変更を行う。基本的にプログラムを用意して一ヶ月間休みなくPCを動かすか、クラウドサービスを利用することになると思う。PCに張り付いて手動で操作してもよい(そのための実施期間?)。やり直しが効かない。
対象
マニュアルの付属資料に対象建物の平面図や機器表と系統図やゾーニング、制御のブロック図と機器効率の曲線などがある。対象はオンライン、オフライン共通と思われる。公平性から考えると参加申し込み後に送付される内容が現在と違ってもおかしくはないと思うが、そこまで配慮しないかもしれない。
- 7階建で延べ床10,000m2くらいのテナントビル
- 人員1000人近くが確率的に動き回る(乱数のシード値は参加者共通)
- 中央熱源式で主な機器はガス焚き吸収式冷温水発生機と冷却塔と空冷モジュールHPで温度成層型の蓄熱槽がある
- 電気室や中央監視室などの空冷PACは対象外
入力
- 設定温度等の制御パラメータを指定する
- 一つ一つ設定するのは大変だがエクセルで一括設定ができる(その他のインターフェースもある)
- オフライン部門の制御パラメータは最大20の日程のグループに分けてそれぞれ設定する。設定ファイルを提出する
- オンライン部門ではリアルタイムに設定値を送ることで独自制御アルゴリズムを実現可能。VPN接続で直接設定する
出力
- 月1回の快適性アンケート
- GUIで表示されるデータの1分間隔のログのcsvファイル
- その他のGUIで表示されない情報は基本的に得られない
- デフォルトの制御に対する省エネ性と快適性の値(目的変数)は毎分得られる
GUI
以下のようなBASを模擬したものが用意されている。


おわりに
電脳建築最適化世界選手権は以下のようなものである。
- 設定温度等を入力して(省エネ性×快適性)の大きさを競う
- 省エネ性や快適性を算出するエミュレータは与えられる
- 誰でも無料で参加可能
- 参加申し込み(4/12まで)
- オフライン部門(6/7~7/7)、膨大な制御パラメータの最適化
- オンライン部門(7/8~8/7)、最適な制御モデルの構築
空調に詳しくない人にも興味を持ってもらえればと思うのだけれど、年間計算最短9時間10分くらいかかるようなので力技の最適化は少しつらいかもしれない。第一回なので運営側も手探りなところが多いと思うけれど盛り上がればいいなと思う。
ModelicaのBuildingsライブラリのHeatTransferを学ぶ_その3 PCMの計算
概要
OpenModelicaでLBNLのBuildingsライブラリを使って熱伝導の計算を学ぶ。間違い等あればいろいろ教えて頂けるとありがたい。
前回は単層壁の1次元熱伝導モデルBuildings.HeatTransfer.Conduction.SingleLayerのPCM以外の部分を見たので今回はPCMの計算部分を確認する。
使用バージョン
- Buildings 5.1.0
PCMの計算方法の概略
基本的に物質は相変化のために熱を使用している間は温度が一定となる。PCM(Phase Change Material)はその性質を利用して利用したい温度帯での見かけの熱容量を大きくして温度を安定させる材料となる。ただし、相変化の温度帯の調整や建材として使用するなどの理由により複数の材料を混ぜることで、相変化の間でもPCMの温度は変化していることが多い。BuildingsライブラリのPCMの計算で参考している文献にあるPCMを30%混ぜた板材の熱量と温度の関係のモデルはだいたい以下のようになる。
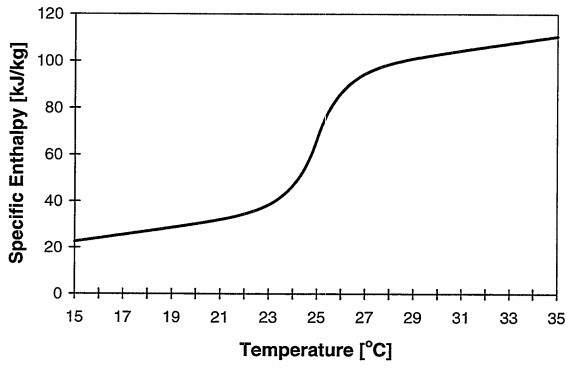
この図は計算モデルを表しているものであり、比熱は固相、液相、固液混相域で同じ値を用いたものであるが、縦軸の比エンタルピー(熱量)と横軸の温度の関係を見ると25℃付近での温度変化に対する必要熱量が大きくなっていることがわかると思う。本来は液相の方がPCMの比熱は少し大きくなるらしい。Buildingsライブラリの実装では比熱や密度や熱伝導率は固相と液相で同じ値を使用している。さらに熱量に関しては比エンタルピーではなく比内部エネルギーを定義して比内部エネルギーと温度の関係としている。内部エネルギーの変化量=エンタルピーの変化量+仕事量なので圧力や体積が変わらない(無視できる範囲内)ならば仕事をせず同じように扱えるということなのだと思う。ちなみに「比」というのは「単位質量あたりの」という意味である。
Cubic Hermite splineについて
Buildingsライブラリでは比内部エネルギーと温度の関係を表すために3次エルミートスプラインを使用している。基本的には固相や液相の時と固液混相のときでそれぞれ傾きの異なる直線としてモデル化したかったのだと思うのだが、おそらく傾きが不連続になると数値計算上収束性が悪くなるなどの問題がでるためにこのような方法をとっているものと考えられる。ちなみに参考文献(上のPCMの資料)では双曲線関数を使用していたようなのだが、どちらがよいのかはよくわからない。3次エルミートスプラインのほうが適当に近似曲線をつくるのは楽そうではある。
3次エルミートスプラインとは以下のようなものである。
- エルミート補間は各点の値と微分を一致させる補間。だいたい3次のスプライン。
- スプラインは区分多項式のこと。区分(点と点の間)毎に数式を定義する。
- 3次式とするのは各区分の両端の値と微分の合計4つの値を条件とすると3次式が一意に定まるから。
数式の内容は英語のWikipediaCubic Hermite splineに書いてあるとおりである。Wikipedeiaの式を今回の実装に対応させて書き直すと以下のようになる。
点(x1,y1) の微分dy/dx1 と点(x2,y2) の微分dy/dx2 が与えられたとき x1 < x < x2 である x に対応する y を求める。仮にx1=0、x2=1であったときにはyの値は以下のようになる。
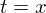
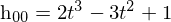
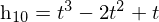
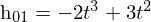
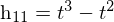
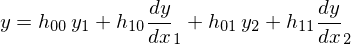
そしてこれにアフィン変換(今回は回転やせん断はなく平行移動と拡大縮小のみ)を施して一般的な形にすると以下のようになる。h00~h11の係数は上の式と同じである。
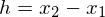
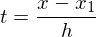
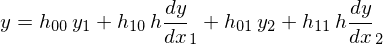
この計算モデルがModelica標準ライブラリで用意されている。微分dy/dxについては自分で用意する必要があるのだが、今回の実装では⊿を各点を結んだ直線の傾きとすると、各点につながる直線の傾きの平均を各点の微分としている。
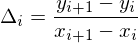
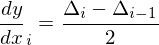
両端については片側にしか直線がないのでその値を使用する。
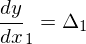
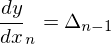
さらに補間に使用する微分の値に補正をかけることで単調性を確保することができる。つまり与えられた点が単調増加や単調減少なら補間した値も単調性を保つようにできるのだ。こちらはBuildingsライブラリで実装されており、以下の論文を参考にしているらしい。
F.N. Fritsch and R.E. Carlson, Monotone piecewise cubic interpolation. SIAM J. Numer. Anal., 17 (1980), pp. 238-246
論文は有料だが同著者の似たような記事でやや古いPDFがあるようだ。また、英語のWikipediaのMonotone cubic interpolationもこの内容である。Wikipediaの図を見れば補正がなぜ必要になるのかがわかると思う。
各点の微分を修正していくのだが、各点をつなぐ直線を左から調べて、両端の点の微分を順次修正していくため、右側の点は次の直線を調べたときに再度微分の値が修正されることになる。
まず直線の傾きが0になる場合はその両端の点の微分は0であるとする。
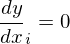
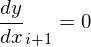
それ以外の場合はまず、単調性を確保させる際に発散させないように以下の条件を調べる。
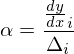
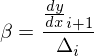
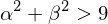
今回の実装ではこれが満たされない区間は補正をしないだけになり警告がでないため、必ず単調性が確保されているわけではないかもしれない。あらかじめ出てきた曲線を調べておいたほうがよさそうである。条件を満たす場合には以下のような処理を行う。
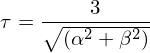
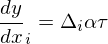
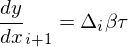
このような処理を繰り返していけば単調性が確保されるらしい。証明までは踏み込まなかったけれど、とりあえずこのようにして計算できるようだ。
初期条件の定義とPCMの計算に用いるパラメータの設定
まず、複数のクラスで共有する定数としてnSupPCMという定数がConductionフォルダのpackage.moに書きこんである。この数は6に設定してあるのだが、PCMの層を物理的に6分割して節点を求めているのではなく、補間に使用する点が6箇所であるという意味である。補間に使用する点数を増やしたい場合には他の部分のコードも修正する必要がでてくるので注意が必要である。
SingleLayerにおいてPCMの計算のみに使用する変数として、3次エルミートスプライン用の比内部エネルギーud(横軸)、温度Td(縦軸)、微分dT_duが要素数6つの配列として定義されており、これらの値を使用して温度を計算することになる。
parameter Modelica.SIunits.SpecificInternalEnergy ud[Buildings.HeatTransfer.Conduction.nSupPCM](
each fixed=false);
parameter Modelica.SIunits.Temperature Td[Buildings.HeatTransfer.Conduction.nSupPCM](
each fixed=false);
parameter Real dT_du[Buildings.HeatTransfer.Conduction.nSupPCM](
each fixed=false,
each unit="kg.K2/J");
近似式は共通のものを使っているものの、温度や比内部エネルギーや熱抵抗や熱容量の定義点の位置は前回の通りであり、場所によってPCMの温度などの状態(固相か液相か固液混相か)は変わり得る。PCMの状態が全ての温度節点で同じ状態である必要はない。
初期条件の定義部分は以下の通り。前回も少し触れたのだが、初期化のときにsteadyStateInitial=trueの場合は微分0の条件が入るが、そうでない場合温度に初期値は与えていても内部エネルギuには値を与えていない。微分0にしても比内部エネルギーを定義するコネクタがないので実質比内部エネルギーの初期条件が定義できていないような気がする。equationの方に温度と比内部エネルギーの関係式があるのでそれを使用して初期温度から比内部エネルギーの初期値を定義してくれているのかもしれない。このあたりを自動でやってくれるのがModelicaのよいところなのだろう。
そして、先ほどの3つの配列に対してmaterialの値とBuildings.HeatTransfer.Conduction.BaseClasses.der_temperature_uという関数を用いて値を定義している。parameterの変数はequationでは値を変更できないが、initial equationの部分であれば数式で値を定義することができるらしい。ensureMonotonicityは3次エルミートスプラインの説明で触れた微分に補正をかけるかどうかの選択でtrueにすると単調性を確保してくれる。
if not material.steadyState then
if steadyStateInitial then
if material.phasechange then
der(u) = zeros(nSta);
else
der(T) = zeros(nSta);
end if;
else
if stateAtSurface_a then
T[1] = T_a_start;
for i in 2:nSta loop
T[i] =T_a_start + (T_b_start - T_a_start)*UA*sum(RNod[k] for k in 1:i-1);
end for;
else // stateAtSurface_a == false
for i in 1:nSta loop
T[i] = T_a_start + (T_b_start - T_a_start)*UA*sum(RNod[k] for k in 1:i);
end for;
end if;
end if;
if material.phasechange then
(ud, Td, dT_du) = Buildings.HeatTransfer.Conduction.BaseClasses.der_temperature_u(
c = material.c,
TSol=material.TSol,
TLiq=material.TLiq,
LHea=material.LHea,
ensureMonotonicity=material.ensureMonotonicity);
else
ud = zeros(Buildings.HeatTransfer.Conduction.nSupPCM);
Td = zeros(Buildings.HeatTransfer.Conduction.nSupPCM);
dT_du = zeros(Buildings.HeatTransfer.Conduction.nSupPCM);
end if;
関数der_temperature_uの中身
Buildings.HeatTransfer.Conduction.BaseClasses.der_temperature_uという関数によってud、Td、dT_duが定義されているので中身を確認する。入力と出力は以下の通り。
入力
| 型 | 名称 | デフォルト値 | 説明 |
|---|---|---|---|
| SpecificHeatCapacity | c | - | 比熱[J/(kg.K)] |
| Temperature | TSol | - | 固相線[K] |
| Temperature | TLiq | - | 液相線[K] |
| SpecificInternalEnergy | LHea | - | 相変化時の潜熱[J/kg] |
| Boolean | ensureMonotonicity | false | Trueの時に強制的に3次エルミートスプラインを単調にする |
出力
| 型 | 名称 | 説明 |
|---|---|---|
| SpecificInternalEnergy | ud[nSupPCM] | 定義点でのud[J/kg] |
| Temperature | Td[nSupPCM] | 定義点でのTd[K] |
| Real | dT_du[nSupPCM] | 定義点でのdT/du[kg.K2/J] |
内部で使用するパラメータとしてscale、Tm1、Tm2がある。
protected parameter Real scale=0.999; parameter Modelica.SIunits.Temperature Tm1=TSol + (1 - scale)*(TLiq - TSol); parameter Modelica.SIunits.Temperature Tm2=TSol + scale*(TLiq - TSol);
関数のアルゴリズムは以下の通り。assert文でBuildings.HeatTransfer.Conduction.nSupPCM==6とTLiq>TSolを要求している。
algorithm
assert(Buildings.HeatTransfer.Conduction.nSupPCM == 6,
"The material must have exactly 6 support points for the u(T) relation.");
assert(TLiq > TSol, "TLiq has to be larger than TSol.");
// Get the derivative values at the support points
ud:={c*scale*TSol,
c*TSol,
c*Tm1 + LHea*(Tm1 - TSol)/(TLiq - TSol),
c*Tm2 + LHea*(Tm2 - TSol)/(TLiq - TSol),
c*TLiq + LHea,
c*(TLiq + TSol*(1 - scale)) + LHea};
Td:={scale*TSol,
TSol,
Tm1,
Tm2,
TLiq,
TLiq + TSol*(1 - scale)};
dT_du := Buildings.Utilities.Math.Functions.splineDerivatives(
x=ud,
y=Td,
ensureMonotonicity=ensureMonotonicity);
近似式に使用する6つの点が何なのかがここで分かった。⊿T=TSol*(1 - scale)と表すと6つの温度が表す点は以下の通り。そしてそれぞれの温度の時の比内部エネルギーudと微分dT_duが定義されている。
| 要素番号 | Td |
|---|---|
| 1 | 固相線-⊿T |
| 2 | 固相線 |
| 3 | 固相線+⊿T |
| 4 | 液相線-⊿T |
| 5 | 液相線 |
| 6 | 液相線+⊿T |
関数splineDerivativesの中身
dT_duを計算しているBuildings.Utilities.Math.Functions.splineDerivativesという関数について見ていく。この関数は三次エルミートスプライン補間に用いる微分を求める関数であり、任意の長さの配列に対して使用することができる。
入力
| 型 | 名称 | デフォルト値 | 説明 |
|---|---|---|---|
| Real | x[:] | - | 横軸の値 |
| Real | y[size(x, 1)] | - | 横軸の値 |
| Boolean | ensureMonotonicity | isMonotonic(y, strict=false) | Trueの時に強制的に3次エルミートスプラインを単調にする |
出力
| 型 | 名称 | 説明 |
|---|---|---|
| Real | d[:] | 微分の値 |
内部で使用する変数として配列の長さn=size(x, 1)、傾きdelta[n - 1]、係数alpha、beta、tauがある。
関数のアルゴリズムは以下の通り。assert文にでてくるBuildings.Utilities.Math.Functions.isMonotonicという関数は与えられた配列a[:]が単調増加または単調減少の場合にtrueを返す関数で、strict=falseの場合にa[n]=a[n+1]となる部分があっても(途中で平らな部分があっても)trueを返すようになっている。Buildings.Utilities.Math.Functions.を省略しているのでModelica標準の関数なのか少しややこしい。ここではxの配列は常に増加しなくてはならず、yはensureMonotonicity=falseならば値に制限がなく、ensureMonotonicity=trueの時は単調増加でも単調減少でもよく途中で同じ値が続くことも許容している。
微分の与え方については、まずn=1のときに微分は0、n=2のときにどちらの点の微分も二つの点を結んだ直線の傾きになる。それ以外ははじめに説明したとおりに実装されておりensureMonotonicity=trueのときに補正を加えるようになっている。
algorithm
if (n>1) then
assert(x[1] < x[n], "x must be strictly increasing.
Received x[1] = " + String(x[1]) + "
x[" + String(n) + "] = " + String(x[n]));
// Check data
assert(isMonotonic(x, strict=true),
"x-values must be strictly monontone increasing or decreasing.");
if ensureMonotonicity then
assert(isMonotonic(y, strict=false),
"If ensureMonotonicity=true, y-values must be monontone increasing or decreasing.");
end if;
end if;
// Compute derivatives at the support points
if n == 1 then
// only one data point
d[1] :=0;
elseif n == 2 then
// linear function
d[1] := (y[2] - y[1])/(x[2] - x[1]);
d[2] := d[1];
else
// Slopes of the secant lines between i and i+1
for i in 1:n - 1 loop
delta[i] := (y[i + 1] - y[i])/(x[i + 1] - x[i]);
end for;
// Initial values for tangents at the support points.
// End points use one-sided derivatives
d[1] := delta[1];
d[n] := delta[n - 1];
for i in 2:n - 1 loop
d[i] := (delta[i - 1] + delta[i])/2;
end for;
end if;
// Ensure monotonicity
if n > 2 and ensureMonotonicity then
for i in 1:n - 1 loop
if (abs(delta[i]) < Modelica.Constants.small) then
d[i] := 0;
d[i + 1] := 0;
else
alpha := d[i]/delta[i];
beta := d[i + 1]/delta[i];
// Constrain derivative to ensure monotonicity in this interval
if (alpha^2 + beta^2) > 9 then
tau := 3/(alpha^2 + beta^2)^(1/2);
d[i] := delta[i]*alpha*tau;
d[i + 1] := delta[i]*beta*tau;
end if;
end if;
end for;
end if;
end splineDerivatives;
Modelica.Constants.small=1.e-60であり、PCが表示する限界の桁数の小さな値という意味らしい。 前回出てきたのはModelica.Constants.eps=1.e-15でこちらは1.0+eps=1.0となる最大の数値だそうなのでそちらでも十分なような気がするというか使い分けがよく分からない。
PCMの比内部エネルギーと温度の計算
初期条件の与え方の確認が終わったので実際の計算部分を確認する。コネクタとのやり取りや分割した各点での熱流の計算は前回確認した通りである。
定常計算のときには比内部エネルギーの変化がなく両端の温度と熱抵抗から各点の温度を計算している。おそらく比内部エネルギーは温度から逆算されている。
非定常計算の場合にはder(u[i]) = (Q_flow[i]-Q_flow[i+1])*mInv[i]とあるように温度ではなく比内部エネルギーの変化量を熱流により定義している。そしてBuildings.HeatTransfer.Conduction.BaseClasses.temperature_uという関数に先ほどの3つの配列と比内部エネルギーを与えて温度を計算している。
equation
port_a.Q_flow = +Q_flow[1];
port_b.Q_flow = -Q_flow[end];
port_a.T-T[1] = if stateAtSurface_a then 0 else Q_flow[1]*RNod[1];
T[nSta]-port_b.T = if stateAtSurface_b then 0 else Q_flow[end]*RNod[end];
for i in 1:nSta-1 loop
T[i]-T[i+1] = Q_flow[i+1]*RNod[i+1];
end for;
// Steady-state heat balance
if material.steadyState then
for i in 2:nSta+1 loop
Q_flow[i] = port_a.Q_flow;
end for;
for i in 1:nSta loop
if material.phasechange then
T[i]=Buildings.HeatTransfer.Conduction.BaseClasses.temperature_u(
ud=ud,
Td=Td,
dT_du=dT_du,
u=u[i]);
else
u[i]=0;
end if;
end for;
else
if material.phasechange then
for i in 1:nSta loop
der(u[i]) = (Q_flow[i]-Q_flow[i+1])*mInv[i];
T[i]=Buildings.HeatTransfer.Conduction.BaseClasses.temperature_u(
ud=ud,
Td=Td,
dT_du=dT_du,
u=u[i]);
end for;
else
for i in 1:nSta loop
der(T[i]) = (Q_flow[i]-Q_flow[i+1])*CInv[i];
end for;
for i in 1:nSta loop
u[i]=0; // u is not required in this case
end for;
end if;
end if;
関数temperature_uの中身
Buildings.HeatTransfer.Conduction.BaseClasses.temperature_uという関数は線形補間や3次エルミートスプライン補間により比内部エネルギーから温度を求める関数である。この関数では与えられた内部エネルギーがどの区間にいるのかを判定しているだけで、実際に温度を計算してるのはBuildings.Utilities.Math.Functions.cubicHermiteLinearExtrapolationという関数である。dT_duの要素数をnSupPCMに指定していない理由がわからないが、動いているプログラムをいじりたくはないのでもやもやする。
入力
| 型 | 名称 | デフォルト値 | 説明 |
|---|---|---|---|
| SpecificInternalEnergy | ud[nSupPCM] | - | 定義点でのud[J/kg] |
| Temperature | Td[nSupPCM] | - | 定義点でのTd[K] |
| Real | dT_du[:] | - | 定義点でのdT/du[kg.K2/J] |
| SpecificInternalEnergy | u | - | 比内部エネルギー[J/kg] |
出力
| 型 | 名称 | 説明 |
|---|---|---|
| Temperature | T | 温度[K] |
関数のアルゴリズムは以下の通り。
algorithm
i := 1;
for j in 1:size(ud,1) - 1 loop
if u > ud[j] then
i := j;
end if;
end for;
T := Buildings.Utilities.Math.Functions.cubicHermiteLinearExtrapolation(
x=u,
x1=ud[i],
x2=ud[i + 1],
y1=Td[i],
y2=Td[i + 1],
y1d=dT_du[i],
y2d=dT_du[i + 1]);
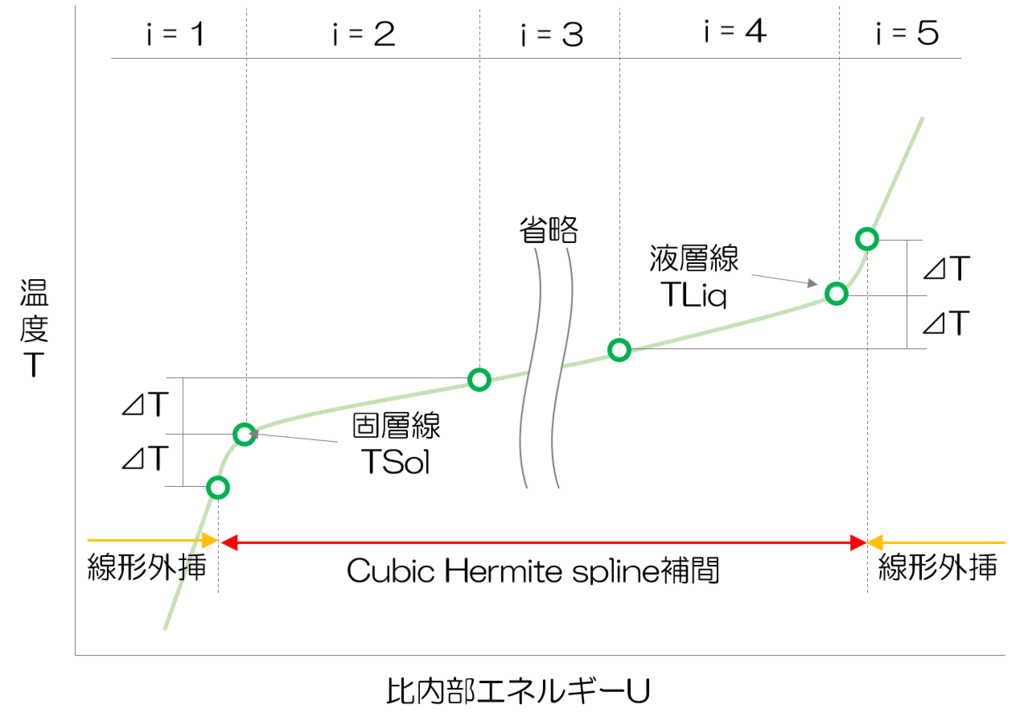
iは6つの点から隣り合う2つの点を選ぶインデックスであり、1から5のどれかになる。そして比内部エネルギーが6つの点の外側にあった場合には線形外挿されることになる。図で表すと以下のようになる。分かりやすさのため⊿Tを大きく書いたが実際は0.01K程度である。傾きの異なる二つの直線を滑らかにつなぐためにこのようにしているのだと思う。
関数cubicHermiteLinearExtrapolationの中身
3次エルミートスプラインは与えられた点の内側の補間のみをするようになっているため、Buildings.Utilities.Math.Functions.cubicHermiteLinearExtrapolation関数では補間に用いる6つの点の外側で線形外挿する処理を行っている。3次エルミートスプラインはModelica.Fluid.Utilities.cubicHermiteという関数を使用して行っている。
入力
| 型 | 名称 | デフォルト値 | 説明 |
|---|---|---|---|
| Real | x | - | 補間値を得たい横軸の値 |
| Real | x1 | - | 補間に用いる横軸の値 |
| Real | x2 | - | 補間に用いる横軸の値 |
| Real | y1 | - | 補間に用いる縦軸の値(x1に対応する値) |
| Real | y2 | - | 補間に用いる縦軸の値(x2に対応する値) |
| Real | y1d | - | 補間に用いる傾き(x1に対応する値) |
| Real | y2d | - | 補間に用いる傾き(x2に対応する値) |
出力
| 型 | 名称 | 説明 |
|---|---|---|
| Real | y | 補間して得た縦軸の値 |
algorithm
if (x > x1 and x < x2) then
y:=Modelica.Fluid.Utilities.cubicHermite(
x=x,
x1=x1,
x2=x2,
y1=y1,
y2=y2,
y1d=y1d,
y2d=y2d);
elseif x <= x1 then
y:=y1 + (x - x1)*y1d;
else
y:=y2 + (x - x2)*y2d;
end if;
関数cubicHermiteの中身
Modelica.Fluid.Utilities.cubicHermiteが3次エルミートスプラインに使用する関数である。これはModelica標準ライブラリの関数なのだがなぜがFluidパッケージの中にある。
入力
| 型 | 名称 | デフォルト値 | 説明 |
|---|---|---|---|
| Real | x | - | 補間値を得たい横軸の値 |
| Real | x1 | - | 補間に用いる横軸の値 |
| Real | x2 | - | 補間に用いる横軸の値 |
| Real | y1 | - | 補間に用いる縦軸の値(x1に対応する値) |
| Real | y2 | - | 補間に用いる縦軸の値(x2に対応する値) |
| Real | y1d | - | 補間に用いる傾き(x1に対応する値) |
| Real | y2d | - | 補間に用いる傾き(x2に対応する値) |
出力
| 型 | 名称 | 説明 |
|---|---|---|
| Real | y | 補間して得た縦軸の値 |
他に内部で使用する変数としてh、t、h00、h01、h10、h11などはじめに確認した式そのままの変数とaux3(tの三乗)やaux2(tの二乗)などの変数がある。アルゴリズムは以下の通り。
algorithm
h := x2 - x1;
if abs(h)>0 then
// Regular case
t := (x - x1)/h;
aux3 :=t^3;
aux2 :=t^2;
h00 := 2*aux3 - 3*aux2 + 1;
h10 := aux3 - 2*aux2 + t;
h01 := -2*aux3 + 3*aux2;
h11 := aux3 - aux2;
y := y1*h00 + h*y1d*h10 + y2*h01 + h*y2d*h11;
else
y := (y1 + y2)/2;
end if;
end cubicHermite;
これで一応すべて確認したことになる。
おわりに
PCMについては実用上はこれで使えるのだと思う。固相と液相の物性値を変えたい場合も比内部エネルギーのように温度との関係式を定義した関数を用意するとよいのかもしれない。ただし、いろいろと計算を細かくしていくと計算量がどんどん膨大になっていきそうな気もする。比内部エネルギーから温度を算出する関数を定義すれば、勝手に温度から比内部エネルギーの算出もしてくれるのはModelicaの便利なところだと思った。
OpenModelicaのバージョンが1.13.1がリリースされていた。replaceableへの対応に関しては1.14以降になったらしい。さらにModelica標準ライブラリも3.2.3が正式リリースになったようなので使ってみてもよいかもしれない。
次回からは窓の計算モデル(Buildings.HeatTransfer.Windows.Window)を見ながら構成を確認したり日射周りの計算などを見たりしていきたいと思う。
PyGemのインストールメモ
概要
PyGemはメッシュモーフィングのライブラリで1400万格子まで対応するらしい。以下の記事をみて面白そうだと思ったのでインストール方法だけメモ。
qiita.com
Linux環境の構築をサボっているので今回はColabにインストールしたけれど、普通の人は自分のLinux環境に入れればいいと思う。
はじめに
Colabに行き「ファイル-Python3の新しいノートブック」を選択。あとは以下のコードを入力してShift+Enterで実行していけばいい。前の処理が終わるのを待つ必要はない。
依存ライブラリのインストール
!pip install numpy scipy matplotlib vtk numpy-stl sphinx nose
Anacondaのインストール
%%bash wget -c https://repo.continuum.io/archive/Anaconda3-5.1.0-Linux-x86_64.sh bash ./Anaconda3-5.1.0-Linux-x86_64.sh -b -f -p /usr/local
Anacondaのアップデート
!conda update -y -n base conda -c defaults
OCCのインストール
!conda install -y -c conda-forge -c dlr-sc -c pythonocc -c oce pythonocc-core==0.18.1 python=3.6
PyGemのインストール
%%bash wget https://github.com/mathLab/PyGeM/archive/v1.1.tar.gz tar -zxvf v1.1.tar.gz cd PyGeM-1.1 2to3 -w ./ python setup.py install
Tutorial1の実行
PyGemがインスト-ルできたので、STLファイルをFFDで変形するサンプルを実行する。
%matplotlib inline
import sys
sys.path.append('/usr/local/lib/python3.6/site-packages/')
sys.path.append('/usr/local/lib/python3.6/site-packages/pygem-1.1-py3.6.egg/')
from pygem import FFDParameters, FFD, StlHandler
params = FFDParameters()
params.read_parameters(filename='./PyGeM-1.1/tests/test_datasets/parameters_test_ffd_sphere.prm')
stl_handler = StlHandler()
mesh_points = stl_handler.parse('./PyGeM-1.1/tests/test_datasets/test_sphere.stl')
fig = stl_handler.plot(plot_file='./PyGeM-1.1/tests/test_datasets/test_sphere.stl')
free_form = FFD(params, mesh_points)
free_form.perform()
new_mesh_points = free_form.modified_mesh_points
stl_handler.write(new_mesh_points, 'test_sphere_mod.stl')
fig = stl_handler.plot(plot_file='test_sphere_mod.stl')
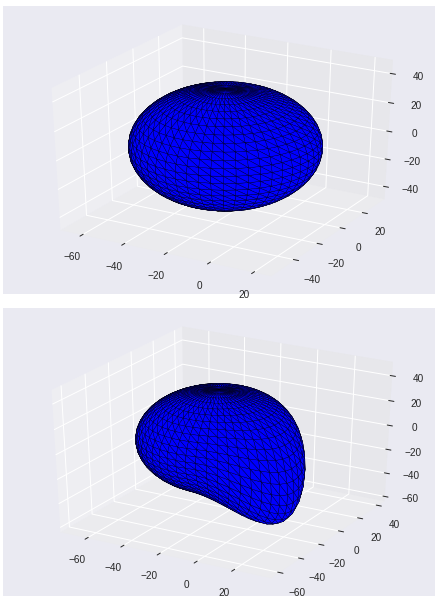
以下のように球体の変形ができている(上が元のSTL、下が変形後のSTL)
おわりに
PyGeM-1.1/pygem/params/の中に変形手法毎のファイルがありそれぞれのread_parametersクラスにどんなパラメータがあるか書いてある。OpenFOAMでの使い方はこの記事が分かりやすかった。ただし、昔は指定していたけれど現在は内部で計算するため@propertyをつけて読取専用としたプロパティがあるので注意。
ModelicaのBuildingsライブラリのHeatTransferを学ぶ_その2
概要
OpenModelicaでLBNLのBuildingsライブラリを使って熱伝導の計算を学ぶ。初心者なのでいろいろ教えて頂けるとありがたい。
すこし間があいてしまったが前回はBuildings.HeatTransferの全体も見てPCM(Phase Change Material、潜熱蓄熱材)を使った簡単な伝熱計算をしてみた。今回は1次元熱伝導計算の基本となるBuildings.HeatTransfer.Conduction.SingleLayerのソースを詳しく確認する。ただし、PCMの計算の細かいところは次回に行う。
使用バージョン
-Buildings 5.1.0
材料の物性値
まずは熱伝導に使用する材料の物性値について確認する。SingleLayerの材料の物性値はreplaceable parameter Data.BaseClasses.Material materialとして定義してあるのだがこう書くものなのだろうか。replaceable record ConMaterial = Data.BaseClasses.MaterialとしてConMaterial materialと書いたほうがよい気がするのだがどうなのだろう。recordにparameterの指定をするのもなくはないのかもしれないけれど、どうなのだろう。問題なく動いているなら下手に手を加えるわけにも行かないのかもしれない。Buildings.HeatTransfer.Data.BaseClasses.Materialに定義されている変数は以下の通り。
| 種類 | 型 | 名称 | デフォルト値 | 説明 |
|---|---|---|---|---|
| パラメータ | Modelica.SIunits.Length | x | - | 材料の厚み |
| パラメータ | Modelica.SIunits.ThermalConductivity | k | - | 熱伝導率 |
| パラメータ | Modelica.SIunits.SpecificHeatCapacity | c | - | 比熱 |
| パラメータ | Modelica.SIunits.Density | d | - | 密度 |
| パラメータ | Real | R(unit="m2.K/W") | - | 熱抵抗 |
| パラメータ | Integer | nStaRef(min=0) | 3 | 参照部材(0.2mのコンクリート)の状態変数の数 |
| パラメータ | Integer | nSta(min=1) | max(1, integer(ceil(nStaReal))) | 材料の実際の状態変数の数 |
| パラメータ | Boolean | steadyState | (c < Modelica.Constants.eps or d < Modelica.Constants.eps) | Trueの時に定常熱伝導で計算するフラグ |
| パラメータ | Real | piRef | 331.4 | 参照部材(0.2mのコンクリート)のx/sqrt(alpha) |
| パラメータ | Real | piMat | if steadyState then piRef else xsqrt(cd/k) | x/sqrt(alpha) |
| パラメータ | Real | nStaReal(min=0) | nStaRef*piMat/piRef | 実数としての状態の数 |
| パラメータ | Modelica.SIunits.Temperature | TSol | - | 固相温度、PCMでのみ使用 |
| パラメータ | Modelica.SIunits.Temperature | TLiq | - | 液相温度、PCMでのみ使用 |
| パラメータ | Modelica.SIunits.SpecificInternalEnergy | LHea | - | 状態変化の潜熱 |
| 定数 | Boolean | ensureMonotonicity | false | Trueの時に微分dT/duを強制的に単調にする |
| 定数 | Boolean | phasechange | false | 材料がPCMの時にTrueにする |
steadyStateのところのModelica.Constants.epsは極小値をあらわす定数で1.e-15である。比熱か密度が0のときに定常としている。また、TSol以降はPCM用の設定で最後の二つの変数の修飾子はparameterではなくconstantになっている。
熱伝導計算に実際に使用するBuildings.HeatTransfer.Data.Solidsの一般的なものは以下のようになっていて、熱抵抗の式とPCM関係の設定をfinalで変更できないようにしている。
record Generic "Thermal properties of solids with heat storage"
extends Buildings.HeatTransfer.Data.BaseClasses.Material(final R=x/k,
final TSol=293.15,
final TLiq=293.15,
final LHea=0,
final phasechange=false);
end Generic;
これに具体的に値を与えるときは以下のようにする。実際に使用するときはこの書き方だけ分かっていればよいと思う。
record Concrete = Buildings.HeatTransfer.Data.Solids.Generic (
k=1.4,
d=2240,
c=840) "Concrete (k=1.4)";
材料の分割数の決定
Buildings.HeatTransfer.Data.SolidsにnStaRef、nSta、piRef、piMat、nStaRealあたりの説明があり、非定常熱伝導の現象の無次元数であるフーリエ数Fo(伝熱量/畜熱量)を使用して材料の物性値と厚みにより分割数を決定している。
フーリエ数は以下のように定義される。

αは熱拡散係数、tは特徴時間、Lは特徴長さである。任意の時間に対して分割数を決定するので、次のようなフーリエ数を用いた定数Πを導入する。

ここで以下のように定数が一致するように各素材の分割数N'(=nStaReal)を決定する。Πx(=piMat)が分割数を求める部材の定数、Nref(=nStaRef=3)とΠref(=piRef=331.4)が参照部材の値。上の式でL=x/Nとして等式を立てていると考えると分かりやすいと思う。

参照部材は0.2mのコンクリート(α=3.64E-7m/s)としており、デフォルトの分割数は3になっている。伝熱現象の解像度がこれと等しくなるようにその他の材料の分割数を決定している。実際にはN'の小数点以下切り上げとしたNx(=nSta=max(1, integer(ceil(nStaReal))))を使用しているのでもう少し細かくなる。なお、実際には等間隔に分割されるとは限らない。また、ここでの分割数が1であり熱伝導の計算で表面に節点を定義する場合は分割数を2として計算する。詳細は熱伝導のところで触れる。定常状態では分割数は関係なくなると思うが、デフォルトでnStaRefと同じ値3になる。
PartialConductorの継承
SingleLayerはPartialConductorを継承している。PartialConductorの内容は以下のシンプルなものでコネクタはHeatPort二つ、面積Aと熱抵抗Rはパラメータで後から何かしら値を与えなければならず、熱コンダクタンスUAや熱貫流率Uはfinalで定義されている。また、equationにてdTが二つのポート間の温度差として定義されている。定常でも非定常でもよいようにするためか、熱容量に関する値は定義されていない。
partial model PartialConductor extends Buildings.BaseClasses.BaseIcon; parameter Modelica.SIunits.Area A; parameter Modelica.SIunits.ThermalResistance R; final parameter Modelica.SIunits.ThermalConductance UA = 1/R; final parameter Modelica.SIunits.CoefficientOfHeatTransfer U = UA/A; Modelica.SIunits.TemperatureDifference dT "port_a.T - port_b.T"; Modelica.Thermal.HeatTransfer.Interfaces.HeatPort_a port_a; Modelica.Thermal.HeatTransfer.Interfaces.HeatPort_b port_b; equation dT = port_a.T - port_b.T; end PartialConductor;
そしてPartialConductorはSingleLayerで継承される際にRを材料に定義された値として指定されている。
extends Buildings.HeatTransfer.Conduction.BaseClasses.PartialConductor( final R=if (material.R < Modelica.Constants.eps) then material.x/material.k/A else material.R/A);
Modelica.Constants.epsは1.e-15なのでこのif文はRの値が0のときには 厚み/熱伝導率/面積、それ以外のときは熱抵抗/面積となるようにしている。Aは先ほど見たようにPartialConductorの持つ変数であり、PartialConductorに与える値の定義にそのまま記述できるらしい。材料の方のRは[m2.K/W]でPartialConductorのRは[K/W]]なので面積で除算をしている。
SingleLayerの計算定義点の設定
計算上の層の分割がどのようになっているのかを確認する。
まず表面に状態を定義するかどうかを指定する変数がある。デフォルトでは両面とも定義するようになっている。stateAtSurface_a=trueとすればT[1]からA面の表面温度を取得できるが、falseの場合はport_a.Tから表面温度を取得するようになる。この変数によって材料の分割位置がかわってくる。
parameter Boolean stateAtSurface_a=true; parameter Boolean stateAtSurface_b=true;
それから分割数に関わる変数がいくつかある。nStaが温度節点の数、nR=nSta+1は熱抵抗の数になる。nSta2が先ほど見た部材で定義した分割数である。定義しなおすとDymolaでエラーが出るらしいがfinalはつけられないのだろうか。表面に温度節点を定義した場合には最低でも2分割になる。
parameter Integer nSta2=material.nSta;
protected
final parameter Integer nSta=
max(nSta2,
if stateAtSurface_a or stateAtSurface_b then 2 else 1);
final parameter Integer nR=nSta+1;
さらに、SingleLayerで定義されている各節点の状態値は以下のとおり。温度(PCMは内部エネルギーも)と熱流が変数としてあり、それを計算するためのパラメータがprotectedの部分に書かれている。protectedとすると例えば他のモデルでSingleLayer sLayを定義したときにsLay.RNod[1]などとして値を参照することができなくなる。Q_flow[nSta+1]はQ_flow[nR]にすればよいのではないかと思う。
| 種類 | 型 | 名称 | 説明 |
|---|---|---|---|
| 変数 | Modelica.SIunits.Temperature | T[nSta] | 温度 |
| 変数 | Modelica.SIunits.HeatFlowRate | Q_flow[nSta+1] | 熱流 |
| 変数 | Modelica.SIunits.SpecificInternalEnergy | u[nSta] | 比内部エネルギー(PCM用) |
| パラメータ | Modelica.SIunits.ThermalResistance | RNod[nR] | 熱抵抗、nR=nSta+1 |
| パラメータ | Modelica.SIunits.Mass | m[nSta] | 質量 |
| パラメータ | Real | mInv[nSta] | 質量の逆数 |
| パラメータ | Modelica.SIunits.HeatCapacity | C[nSta] | 熱容量 |
| パラメータ | Real | CInv[nSta] | 熱要路湯の逆数 |
これらの変数が層のどの範囲を受け持っているのかを確認する。下の方に図にまとめたのでそちらを先に参照したほうがよいかもしれない。
まずは熱抵抗の設定、それぞれの表面に温度節点を定義しているのかどうかで変わり、表面に節点があるときは材料と反対側の抵抗は使わないので0にしている。それ以外は表面が半分の抵抗になることで変わらない。
parameter Modelica.SIunits.ThermalResistance RNod[nR]=
if (stateAtSurface_a and stateAtSurface_b) then
if (nSta==2) then
{(if i==1 or i==nR then 0 else R/(nSta-1)) for i in 1:nR}
else
{(if i==1 or i==nR then 0 elseif i==2 or i==nR-1 then R/(2*(nSta-2)) else R/(nSta-2)) for i in 1:nR}
elseif (stateAtSurface_a and (not stateAtSurface_b)) then
{(if i==1 then 0 elseif i==2 or i==nR then R/(2*(nSta-1)) else R/(nSta-1)) for i in 1:nR}
elseif (stateAtSurface_b and (not stateAtSurface_a)) then
{(if i==nR then 0 elseif i==1 or i==nR-1 then R/(2*(nSta-1)) else R/(nSta-1)) for i in 1:nR}
else
{R/(if i==1 or i==nR then (2*nSta) else nSta) for i in 1:nR};
次に温度の設定。指定した初期温度で定常条件での温度を指定している。先ほど定義した抵抗の値を使っているので上の図の位置に温度節点があると考えられる。T_a_startとT_b_startは温度の初期値を決めるパラメータで293.15「K](20℃)がデフォルト値である。cateは配列をつなげて第一引数で指定した次元の配列を作る関数なのだが、ここの数式は場合分けしているものの、別にelse以降の式だけで問題ないように思うのだけれど違うのだろうか。(stateAtSurface_a=trueならばRNod[1]=0)
Modelica.SIunits.Temperature T[nSta](start=
if stateAtSurface_a then
cat(1,
{T_a_start},
{(T_a_start + (T_b_start - T_a_start)*UA*sum(RNod[k] for k in 1:i-1)) for i in 2:nSta})
else
{(T_a_start + (T_b_start - T_a_start)*UA*sum(RNod[k] for k in 1:i)) for i in 1:nSta},
each nominal=300);
次に熱容量関係の設定。ここは質量mを設定して残りのmInv、C、CInvはmを演算しているだけである。面積×厚み×密度を分割しており表面に温度節点を定義していれば表面と表面から2番目の層が他の半分の厚さになっている。
parameter Modelica.SIunits.Mass m[nSta]=
(A*material.x*material.d) *
(if (stateAtSurface_a and stateAtSurface_b) then
if (nSta==2) then
{1/(2*(nSta-1)) for i in 1:nSta}
elseif (nSta==3) then
{1/(if i==1 or i==nSta then (2*(nSta-1)) else (nSta-1)) for i in 1:nSta}
else
{1/(if i==1 or i==nSta or i==2 or i==nSta-1 then (2*(nSta-2)) else (nSta-2)) for i in 1:nSta}
elseif (stateAtSurface_a and (not stateAtSurface_b)) then
{1/(if i==1 or i==2 then (2*(nSta-1)) else (nSta-1)) for i in 1:nSta}
elseif (stateAtSurface_b and (not stateAtSurface_a)) then
{1/(if i==nSta or i==nSta-1 then (2*(nSta-1)) else (nSta-1)) for i in 1:nSta}
else
{1/(nSta) for i in 1:nSta});
残りの定義は以下の通り。熱容量は質量×比熱である。
final parameter Real mInv[nSta]=
if material.steadyState then zeros(nSta) else {1/m[i] for i in 1:nSta};
final parameter Modelica.SIunits.HeatCapacity C[nSta] = m*material.c;
final parameter Real CInv[nSta]=
if material.steadyState then zeros(nSta) else {1/C[i] for i in 1:nSta};
分かりにくいので図にすると以下のようになる。表面温度を設定した部分では熱容量の配分と熱抵抗の配分が一致していないような気がする。説明にもそうしていると書いてあるのでバグではないようなのだけれど少しもやもやする。熱抵抗の中心で熱容量を分割したほうがモデルとしてわかりやすいのではないだろうか。

initial equation
assert文があり、分割時の熱抵抗と熱容量の合計値が間違っていないかをチェックしている。
温度は変数を定義する際にstartで値を指定しても結局initial equationを定義してあげないと警告がでるようなので、再度定義をしていると思われる。steadyStateInitialは初期化条件を両端の温度から定常条件で与えるかを選ぶ変数でtrueの時に全ての節点の温度の時間微分が0という条件となる。そうでない場合は先ほどと同じである。この違いはsteadyStateInitial=trueのときには両端の値はコネクタから受け取ったものになるのだろうか。
内部エネルギーuの定義はないのだけれど、Modelica.SIunits.SpecificInternalEnergy u[nSta](each nominal=270000)の270000を使用するのだろうか。今回は使用しないが、PCMであっても特に定義していないように思う。何を定義するのかは独立変数の数だけにしないといけないのかもしれない。ud、Td、dT_duはPCM以外では使用しないので0が入っている。これらはparameterなのだけれどまとめて関数で値を設定するのでこちらで定義していると思われる。
assert(abs(sum(RNod) - R) < 1E-10, "Error in computing resistances.");
assert(abs(sum(m) - A*material.x*material.d) < 1E-10, "Error in computing mass.");
// The initialization is only done for materials that store energy.
if not material.steadyState then
if steadyStateInitial then
if material.phasechange then
der(u) = zeros(nSta);
else
der(T) = zeros(nSta);
end if;
else
if stateAtSurface_a then
T[1] = T_a_start;
for i in 2:nSta loop
T[i] =T_a_start + (T_b_start - T_a_start)*UA*sum(RNod[k] for k in 1:i-1);
end for;
else // stateAtSurface_a == false
for i in 1:nSta loop
T[i] = T_a_start + (T_b_start - T_a_start)*UA*sum(RNod[k] for k in 1:i);
end for;
end if;
end if;
end if;
if material.phasechange then
(ud, Td, dT_du) = Buildings.HeatTransfer.Conduction.BaseClasses.der_temperature_u(
c = material.c,
TSol=material.TSol,
TLiq=material.TLiq,
LHea=material.LHea,
ensureMonotonicity=material.ensureMonotonicity);
else
ud = zeros(Buildings.HeatTransfer.Conduction.nSupPCM);
Td = zeros(Buildings.HeatTransfer.Conduction.nSupPCM);
dT_du = zeros(Buildings.HeatTransfer.Conduction.nSupPCM);
end if;
equation
コネクタから熱流を受け取る(熱流の向きはi→i+1の方向)
port_a.Q_flow = +Q_flow[1];
port_b.Q_flow = -Q_flow[end];
コネクタから温度を受け取る、表面に節点があればそのまま、なければ定常計算で端の節点の温度を計算する。
port_a.T-T[1] = if stateAtSurface_a then 0 else Q_flow[1]*RNod[1];
T[nSta]-port_b.T = if stateAtSurface_b then 0 else Q_flow[end]*RNod[end];
定常のときはT[:]の計算、非定常のときはQ_flow[:]の計算になる。両端はコネクタから受け取った値である。
for i in 1:nSta-1 loop
T[i]-T[i+1] = Q_flow[i+1]*RNod[i+1];
end for;
定常計算のときは全ての熱流が等しいという条件で上のQ_flow[:]の計算Q_flow[i] = port_a.Q_flow、非定常のときはT[:]の計算der(T[i]) = (Q_flow[i]-Q_flow[i+1])*CInv[i]。比内部エネルギーは使わないので0を与えている。PCMの計算については次回確認してい。
表面に節点を定義としたところにFixedTemperatureを直接つなぎ込むと、その固定温度とここで計算する温度が一致させられずエラーになるので注意が必要である。
// Steady-state heat balance
if material.steadyState then
for i in 2:nSta+1 loop
Q_flow[i] = port_a.Q_flow;
end for;
for i in 1:nSta loop
if material.phasechange then
// Phase change material
T[i]=Buildings.HeatTransfer.Conduction.BaseClasses.temperature_u(
ud=ud,
Td=Td,
dT_du=dT_du,
u=u[i]);
else
// Regular material
u[i]=0; // u is not required in this case
end if;
end for;
else
// Transient heat conduction
if material.phasechange then
// Phase change material
for i in 1:nSta loop
der(u[i]) = (Q_flow[i]-Q_flow[i+1])*mInv[i];
// Recalculation of temperature based on specific internal energy
T[i]=Buildings.HeatTransfer.Conduction.BaseClasses.temperature_u(
ud=ud,
Td=Td,
dT_du=dT_du,
u=u[i]);
end for;
else
// Regular material
for i in 1:nSta loop
der(T[i]) = (Q_flow[i]-Q_flow[i+1])*CInv[i];
end for;
for i in 1:nSta loop
u[i]=0; // u is not required in this case
end for;
end if;
end if;
おわりに
とりあえず単層壁の非定常熱伝導の計算をみていった。計算モデルの内容はしっかり分かったのだが、1次元の熱伝導計算もこだわるといろいろでてくるのだなぁと思った。
層の分割数の決定方法については勉強になったが、結局分割幅が表面の節点の定義状況によって変わってしまうので本当にこれでいいのだろうかという気になった。それから現状では場合分けを理解するのに少し苦労するのではないかと思う。まず熱容量を等分割して熱容量のセル中心に温度節点を配置、熱抵抗分割位置に対応するように配置し、表面に温度節点があるときは端のセルの半分の熱容量を表面に与えるという仕組みだった。このとき熱抵抗の定義はかわらないため、熱容量の扱いのみが変わることになる。
次回は同じモデルの中のPCMの計算部分について見ていく。PCMでは相変化する際にはスプライン補間を使いながら内部エネルギーから温度を読み取るようになっている。このやり方は熱水分同時移動の物性値などにも転用できるのではないかなぁと思うけれどどうなんだろう。次回のModelica勉強会のネタにできればいいのだけれどどうなることやら。次回は来年になりそうだけれどマイペースに頑張ります。